Atheist Foundation of Australia
- To encourage and to provide a means of expression for informed free-thought on philosophical and social issues.
- To safeguard the rights of all non-religious people.
- To serve as a focal point for the community of non-religious people.
- To offer verifiable information in place of superstition and to promote logic and reason.
- To promote atheism.
Campaigns
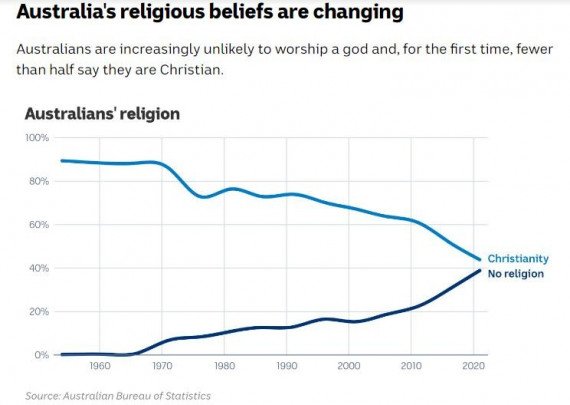
Census No Religion
The current census data does not accurately reflect our country’s religious views.
This is due to a large number of Australians marking that they belong to a religion in the census when in fact they no longer practise or hold those beliefs.
Census data is used by the government and many other organisations to inform a wide range of important decisions from the amount of public funding religious organisations receive, to the voice and influence religion is given in public affairs and media.
The next Australian Census will be held on Tuesday 10th August 2021 and we need it to accurately reflect what Australians truly believe.
So, when you’re filling in the census and you come to the question of religion, this is your chance to think carefully and decide whether you still see yourself as religious.
If you don’t see yourself as religious anymore, this census, mark ‘No Religion’.

Our Philosophy
The Atheist Foundation of Australia recognises the scientific method as the only rational means toward understanding reality. To question and critically examine all ideas, testing them in the light of experiment, leads to the discovery of facts.
As there seems to be no scientific evidence for supernatural phenomena, atheists reject belief in ‘God’, gods, and other supernatural beings. The universe, the world in which we live, and the evolution of life seem to be entirely natural occurrences.
No personality or mind can exist without the process of living matter to sustain it. We have only one life – here and now. All that remains after a person dies is the memory of their life and deeds in the minds of those who remain.
Atheists reject superstition and prejudice along with the irrational fears they cause. We recognise the complexity and interdependence of life on this planet. As rational and ethical beings we accept the challenge of making a creative and responsible contribution to life.